Sometimes I make cool videos in my research. This page is a small collection of the cooler ones I’ve made for various research topics over the years.

Warning: Each of the videos below is approximately 1MB.

Interpretation of Learned Dynamics

Searching for a model that integrates $u^{k+1} = A u^k$ from snapshots can be performed by performing gradient descent on \begin{equation} \min_A \sum_{batch} | \hat{u}^{k+1} - A u^{k} |^2_F \end{equation} For the wave equation, the known continuous in time and space operator is, \begin{equation} \left( \begin{array}{c} \dot{u}\\ \dot{v} \end{array} \right) = \left[ \begin{array}{cc} 0 & I \\ \nabla^2 & 0 \end{array} \right] \left( \begin{array}{c}u\\ v\end{array} \right) \end{equation} The evolution of the discrete linear operator on the second order system is animated below. The intermediate models are used to try to solve the system as it trains.

The structure of the operator evolves as we look at the weights of $A$. The bottom left quadrant learns something like the discrete representation of the wave equation—but embedded inside of a discrete integrator. Extracting the continuous-in-time operator requires more work.

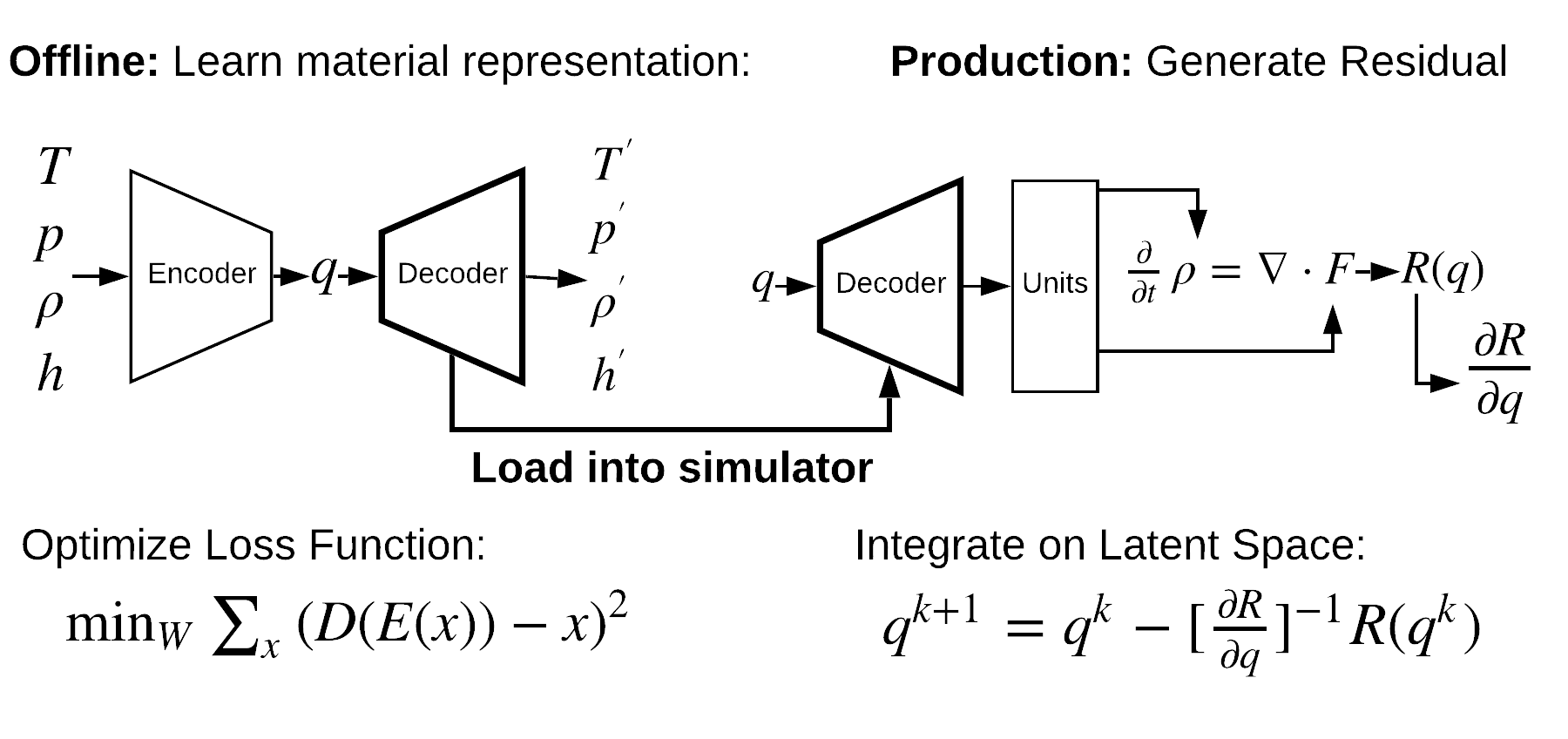
Equation of State Reparameterization with Unsupervised Phase Labeling

An autoencoder is used to learn a new representation of complex multiphase equations of state. Below is an animation of the training process on a dataset of water spanning solid, liquid, gas, and the supercritical regime, without phase labels. “Phases” are learned as features that select different curve fits.

The trained model is inserted directly into balance laws, building differential algebraic equations on the latent space that can be solved easily (with automatic differentiation.)

Large Deformation in Electromechanical Devices

This example is a microelectromechanical “fan” actuated by a piezoelectric element on the rightside. The mechanical deformation is solved only in the body, and the electromagnetic fields are solved everywhere. The mesh in the surrounding vacuum is moved to accomodate the large deformations of the fan. The theory and algorithms for this simulation was published in Abali and Queiruga, 2018 and Github: https://github.com/afqueiruga/EMSI-2018.

Hydraulic Fracture Extension

A peridynamics model is used to simulate the hydraulic fracturing process fully coupled to finite-element models of porous flow and fracture flow. The growth of the fracture is modeled by weakening and breaking bonds between peridynamic material points in response to the strain. Fluid injection drives the growth of the initial hydraulic fracture and interacting with a natural fracture to the left. Below the peridynamic points are plotted, colored by the y displacement, and the fields for matrix-pore pressure and fracture pressure on the left. The fracture is dynamically remeshed.

But remember, videos are not results! Even though it looks cool, it turns out this method for solving mechanics does not work. The video shows oscillations that form vertical stripes in the point coloring, which motivated the study published in “Numerical experiments on the convergence properties of state-based peridynamic laws and influence functions in two-dimensional problems” and PeriFlakes. A hyperparameter search on possible Peridynamics schemes failed to find a method that passed the most basic tests, despite producing plausible illustrations and videos.

Microstructure Simulation of Electronic Textiles

A woven-beam finite element simulation with multiphysics contacts is used to perform material property prediction.

Electronic Textiles in Ballistic Impacts

High strength textiles are a fundamental component of armors in multiple applications, where they are coupled with metal and ceramic plates and various other systems. In this research, the effect of applying electromagnetic fields to a ballistic fabric undergoing impact is explored, wherein an external magnetic field induces deformation in an electrified sheet to influence the behavior of the projectile.

Image Processing in Impact Experimentation

A silicone ballistic block was embedded with a grid using thread and ink. A baseball is fired at the block, and custom image processing software is used to track the grid. A better camera is needed to be able to follow all of the points.

DEM Simulations of a Granular Shear Cell

A discrete Element simulation is used to obtain local flow properties of a granular media inside of an anular shear cell. Particles are affixed to the inside wheel of the shear cell that rotates at a constant rate. Contacts between particles and between particles and the boundary resolved by a soft-sphere Hertzian spring-dashpot normal force and a history-based frictional force.